[1. E. Aamari, J. Kim, F. Chazal, B. Michel, A. Rinaldo, L. Wasserman]
In preparation (Expected on Dec. 2016).
INRIA Associated Team between DataShape and Carnegie Mellon University (CMU)
| With the recent explosion in the amount and variety of available data, identifying, extracting and exploiting their underlying geometric structures has become a problem of fundamental im- portance for data analysis and statistical learning. On the theoretical side, the topological and geometric properties of data are of great help to analyze them and can be used for further learn- ing or classification tasks. On the algorithmic and applied side, understanding the underlying geometric structure of data can help face the so-called curse of dimensionality phenomenon, and down the road lead to drastic improvements in the complexity of algorithms. There exist various statistical and machine learning methods that intend to uncover the geometric structure of data, such as clustering, manifold learning and non linear dimensionality reduction, principal curves, sets estimation, to name a few. Most of them assume the underlying structure to have a very simple geometry, diffeomorphic to a disc or isometric to an open set of a Euclidean space. Furthermore the only topological information they seek for is connectivity. On another hand, with the emergence of distance based approaches and persistent topology, geometric inference and computational topology have recently known an important development. New mathematically well-founded theories gave birth to the field of Topological Data Analysis (TDA) which is knowing an increasing interest both in academy and industry. So far the obtained results rely mostly on deterministic assumptions which are not satisfactory from a statistical viewpoint. As a consequence the corresponding methods remain exploratory and do not benefit from a sound probabilistic framework. Despite a few notable attempts to overcome this issue, the development of a statistical approach to Topological Data Analysis is still in its infancy. As data are becoming larger and larger, the development of rigorous statistical approaches for TDA but also of algorithmic tools implementing them are challenges of fundamental importance that we intend to address. |
| Our conviction, at the root of this project, is that there is a real need to combine statistical and topological/geometric approaches in a common framework, in order to face the challenges raised by the inference and the study of topological and geometric properties of the wide variety of larger and larger available data. We are also convinced that these challenges need to be addressed from both the mathematical side and the algorithmic/application side. Our main objectives for the three years are two-fold. First on the theoretical side, we intend to set up and develop the mathematical and algorithmic foundations of Statistical Topological Data Analysis (Statistical TDA); second, we intend to develop software packages implementing state-of-the-art methods and making our tools accessible and easy to use to a broad audience of data scientists. |
| 1. Mathematical foundations of Statistical TDA. Our objective is to show that, thanks to stability properties coming from geometric inference and persistent homology theory, topological and geometric properties of data, such as e.g. persistence diagrams, can be efficiently inferred in various statistical settings. We intend to propose various estimators coming with statistical guarantees (convergence results, convergence rates,...) to which classical statistical tools and constructions can be applied (bootstrap, confidence bands, tests,...). Our ultimate objective is to provide a well-founded and effective statistical toolbox for the understanding of the topology and geometry of data. |
| 2. Efficient easy-to-use software tools and applications. The DataShape group recently released Gudhi , a C++ library -- supported by the ERC project of Jean-Daniel Boissonnat -- dedicated to state-of-the-art computational topology and geometry in high dimensional spaces. On the other hand, building on the first results of our starting collaboration, the CMU group recently released a R package, TDA for doing statistical analysis of persistent homology. We will combine our software developments efforts to design software tools for Statistical TDA that include robust and efficient computational topology algorithms for statistical TDA through a simple interface that can be used by data scientists without strong expertize in topology and geometry. We also intend to use this tools to validate our methods on real data. |
|
|
Approximation and geometry of the reach [1. E. Aamari, J. Kim, F. Chazal, B. Michel, A. Rinaldo, L. Wasserman] In preparation (Expected on Dec. 2016). |
|
|
The distance-to-a-measure signature for a bootstrap test of isomorphism between metric measure spaces [1. C. Brecheteau] In preparation (Expected on Dec. 2016). |
|
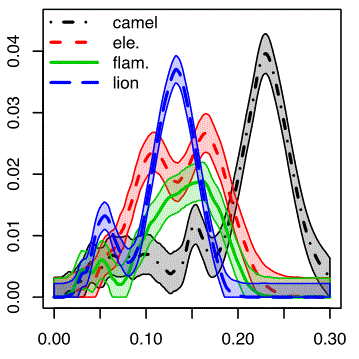
Subsampling Methods for Persistent Homology [F. Chazal, B.T. Fasy, F. Lecci, B. Michel, A. Rinaldo, L. Wasserman] In proc. International Conference on Machine Learning (ICML 2015). |
|
Robust Topological Inference: Distance To a Measure and Kernel Distance [F. Chazal, B.T. Fasy, F. Lecci, B. Michel, A. Rinaldo, L. Wasserman] Submitted. |