Display paper

Comparing points on 3D shapes is among the fundamental operations in shape analysis. To facilitate this task, a great number of local point signatures or descriptors have been proposed in the past decades. However, the vast majority of these descriptors concentrate on the local geometry of the shape around the point, and thus are insensitive to its connectivity structure. By contrast, several global signatures have been proposed that successfully capture the overall topology of the shape and thus characterize the shape as a whole. 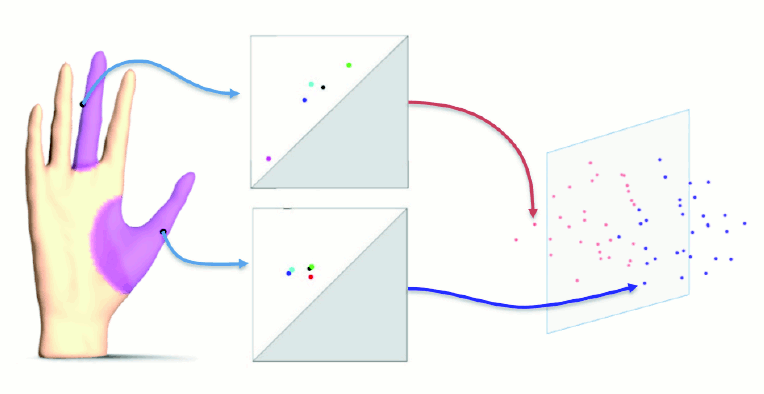In this paper, we propose the first point descriptor that captures the topology structure of the shape as ‘seen’ from a single point, in a multiscale and provably stable way. We also demonstrate how a large class of topological signatures, including ours, can be mapped to vectors, opening the door to many classical analysis and learning methods. We illustrate the performance of this approach on the problems of supervised shape labeling and shape matching. We show that our signatures provide complementary information to existing ones and allow to achieve better performance with less training data in both applications.