
The four spheres have radius 80 and centers of coordinates (0,0,0), (72,-171,-45), (-92,-130,38) and (-126,33,129). Notice that 4 of the lines touch the spheres in one order and 4 in an other one.
Given 4 spheres, assuming there is only a finite number of lines tangent to all of them, how large can this number be? There is a well-known upper-bound of 12, and a well-known lower bound of 12 with unit balls. If we restrict the problem to disjoint unit balls, it is open. The best known upper bound is still 12, and the best known lower bound is 8 with the following example.

The four spheres have radius 80 and centers of coordinates
(0,0,0), (72,-171,-45), (-92,-130,38) and (-126,33,129). Notice that 4 of
the lines touch the spheres in one order and 4 in an other one.
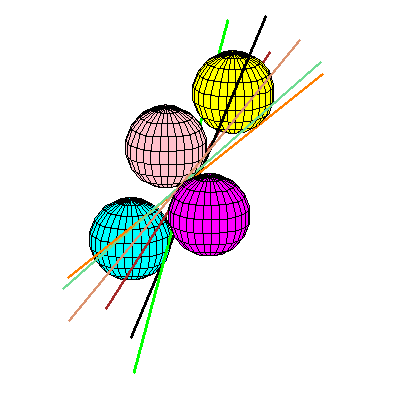
With 4 spheres of radius 80 and centers (0,0,0), (-72,138,59),
(-82,21,172) and (-236,62,254), there are only 6 lines tangent to all the
balls, but all 6 touch the spheres in the same order.
These two exemples were obtained by generating 4 random balls and checking for lines tangent to them. The program never generated sets of balls with lines tangent to them in 3 different orders, or more than 8 tangents in total, and whenever there were 6 tangents in the same order, there were no other tangents.
The pictures were done in maple using code by Frank Sottile.